728x90
스칼라와 벡터
- 평면의 좌표 (x,y)는 두 실수 x와 y를 결합해 만들어진다. 그렇기 때문에 좌표의 연산은 실수가 지니는 연산의 성질을 바탕으로 설계돼야 한다.
- 두 개 이상의 실수를 곱집합으로 묶어 형성된 집합을 공리적 집합론의 관점에서 규정한 것을 **벡터 공간(Vector Space)**이라고 하며, 벡터 공간의 원소를 **벡터(Vector)**라고 한다.
- 공리적 집합론의 관점에서는 특정한 수 집합을 지칭하지 않고 연산이 갖는 성질만 다루기 때문에, 좌푯값으로 사용하는 x와 y를 실수로 규정하기 보다 체의 구조를 지니는 집합, 즉 체 집합의 원소로 규정한다. 이렇게 체의 구조를 가지는 수 집합의 원소를 스칼라(Scalar)라고 부른다.
- 집합의 개념인 벡터 공간을 표기할 때는 주로 대문자 V를 사용하고, 이의 원소인 벡터는 소문자 →v 로 표기한다( v위에 화살표)
벡터 공간의 연산
- 공리적 집합론의 관점에서 정의된 벡터 공간은 두 가지 기본 연산이 존재한다
- 벡터와 벡터의 덧셈(줄여서 벡터의 합으로 부른다)
- v1+v2 = (x1, y1) + (x2, y2) = (x1 + x2 , y1 + y2)
- (화살표는 생략)
- 스칼라와 벡터의 곱셈(줄여서 스칼라 곱셈이라고 부른다)
- a • v = a • (x, y) = (a • x , a • y)
- 체가 갖는 연산의 성질에 기반해 벡터 공간의 연산이 갖는 성질은 8가지로 정리하고 이를 ‘벡터 공간의 공리’ 라고 한다.
- 벡터와 스칼라의 곱을 표현하기 위해 사용한 스칼라 곱셈은 스칼라배 라고도 불린다. 스칼라곱이라는 용어도 있는데, 이는 스칼라 곱셈과 다른 연산이며 내적을 의미한다.
- 벡터의 합 연산은 평면의 점을 각 축에 대해 독립적으로 평행 이동시키는 작업

벡터의 크기와 이동
- 수의 크기는 원점으로부터 거리를 의미하며 절댓값 기호를 사용해 구할 수 있다.
- 벡터의 크기도 동일하게 원점으로부터 최단 거리를 의미한다.
- 원점과 벡터를 연결해 직각삼각형을 기린 후 , 피타고라스 정리를 사용해 거리를 측정한다.
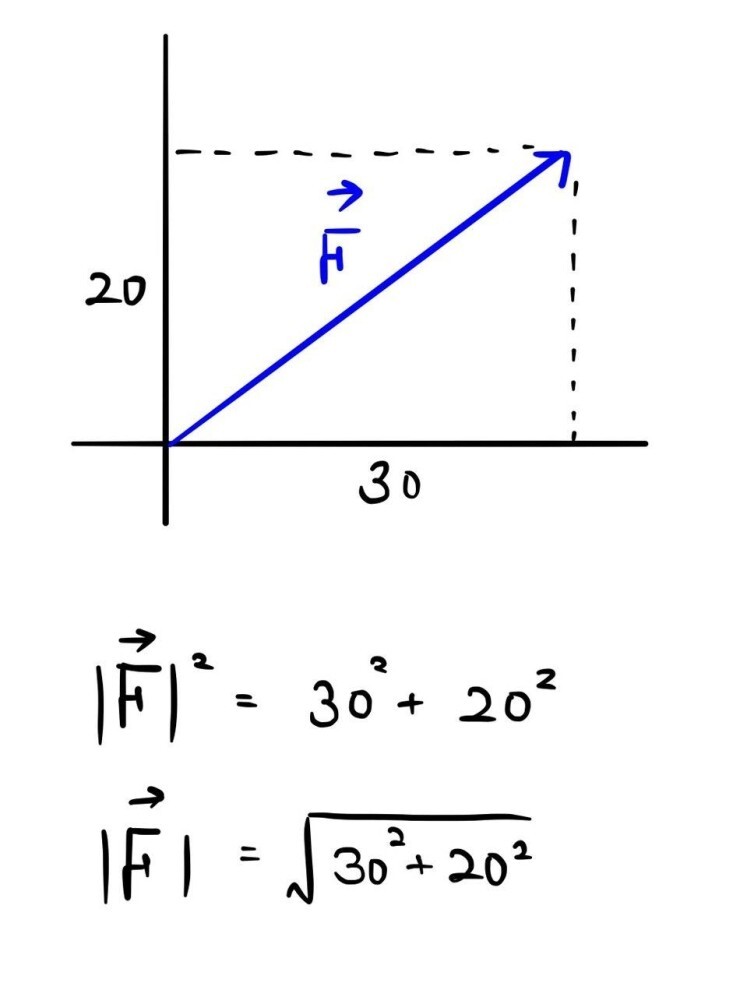
- 벡터의 크기는 노름(Norm) 이라는 용어로 부르기도 한다.
- 크기가 1인 벡터를 단위 벡터(Unit Vector)라고 한다.
- 단위 벡터는 벡터의 크기를 측정하는 기준이 되며, 응용식을 전개하는 데 자주 사용된다.
- 단위 벡터는 모자 기호(Hat)을 씌워 표시
- 임의의 벡터를 크기가 1인 단위 벡터로 다듬는 작업을 정규화(Normalize) 라고 부른다.
728x90
'Computer > 게임 수학' 카테고리의 다른 글
| 5. 벡터의 결합과 생성 (0) | 2023.02.06 |
|---|---|
| 3. 데카르트 좌표계 (0) | 2023.01.31 |
| 2. 함수 (0) | 2023.01.26 |
| 1. 수와 집합 (2) | 2023.01.26 |
| 게임 수학의 구성 (0) | 2023.01.13 |